Example of Information gain

Example

A general framework for growing a decision tree is as described below. Start with a tree with a single leaf (the root) and assign this leaf a label according to a majority vote among all labels over the training set. Now perform a series of iterations. On each iteration, we examine the effect of splitting a single leaf. Now define some "gain" measure that quantifies the improvement of information, or in other words reduction of entropy due to this split. Then, among all possible splits, either choose the one that maximizes the gain and performs it, or choose not to split the leaf at all. In the following, we provide a possible implementation. It is based on a popular decision tree algorithm known as "ID3" (short for "Iterative Dichotomizer 3"). The algorithm works by recursive calls, with the initial call being ID3 and returns a decision tree.

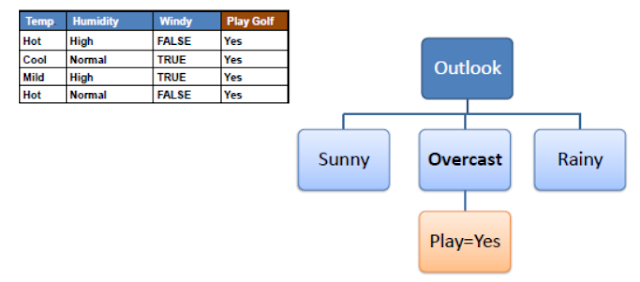
Let’s consider the following example of whether golf will be played or not respective with weather conditions

•  Constructing a decision tree is all about finding an attribute that returns the highest information gain

•     We want the most homogeneous branches

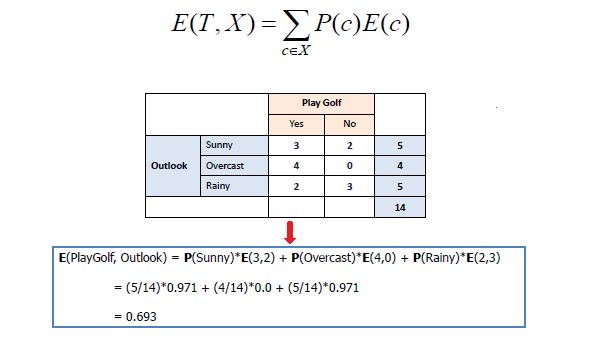
To build a decision tree, we need to calculate two types of entropy using frequency tables as  follows: a) Entropy using the frequency table of one attribute: b) Entropy using the frequency table of two attributes: in the following table we will consider  all three conditions for the output yes r no. count all 'yes' and 'No '  for sunny, overcast, rainy  and put in tabular form as shown below  Information Gain The information gain is based on the decrease in entropy after a dataset is split on an attribute. (i.e., the most homogeneous branches). Step 1: Calculate the entropy of the target. the target may be any of three sunny, overcast, rainy. we have  done an example for sunny as, Step 2: ·        The dataset is then split into the different attributes. (temp, humidity, windy) ·        The entropy for each branch is calculated. (look at the following table) ·        Then it is added proportionally, to get total entropy for the split ·         The resulting entropy is subtracted from the entropy before the split Step 3: Choose attribute with the largest information gain as the decision  node,  divide the dataset by its branches and repeat the same process on every branch. Step 4a:  A branch with the entropy of 0 is a leaf node. Step 4b:  A branch with entropy more than 0 needs further splitting. Decision Tree to Decision Rules A decision tree can easily be transformed to a set of rules by mapping from the root node to the leaf nodes one by one. Decision Trees - Issues Working with continuous attributes (binning) Avoiding overfitting Super Attributes (attributes with many unique values) Working with missing values We will see how to resolve all issues  later in coming blogs Reference: http://www.saedsayad.com/decision_tree.htm