Why linear
regression is not useful in classification problem?
In linear regression the Y
variable is always a continuous variable (i.e. real value either yes or no). If
suppose, the Y variable was categorical (probability of values), using linear
regression model is useless. Logistic regression can be used to model and
solve such problems, also called as binary classification problems.
INTRODUCTION
Logistic regression is supervised learning method. Under supervised
learning techniques, the learning models that are categorized under
statistical methods are instance-based learning methods Bayesian
learning methods and regression analysis. Let us focus on
regression analysis and other related regression models. Regression
analysis is known to be one of the most important statistical techniques.
As mentioned, it is a statistical methodology that is used to measure the
relationship and check the validity and strength of the relationship
between two or more variables. Traditionally, researchers, analysts, and
traders have been using regression analysis to build trading strategies to
understand the risk contained in a portfolio. Regression methods are used
to address both classification and prediction problems.
The method serves two purposes: (1) it can
predict the value of the dependent variable for new values of the independent
variables, and (2) it can help describe the relative contribution of each
independent variable to the dependent variable, controlling for the influences
of the other independent variables. The four main multi-variable methods used in
health science are linear regression, logistic regression, discriminant
analysis, and proportional hazard regression. The four multi-variable methods
have many mathematical similarities but differ in the expression and format of the
outcome variable. In linear regression, the outcome variable is a continuous
quantity, such as blood pressure. In logistic regression, the outcome variable
is usually a binary event, such as alive versus dead, or case versus control.
In discriminant analysis, the outcome variable is a category or group to which
a subject belongs. For only two categories, discriminant analysis produces
results similar to logistic regression. The logistic regression is the most popular
multi-variable method used in health science (Tetrault, Sauler, Wells, & Concato,
2008). In this article logistic regression (LR) will be presented from basic
concepts to interpretation.
MATHEMATICAL MODEL
Logistic regression sometimes called the
logistic model or logit model, analyzes the relationship between multiple
independent variables and a categorical dependent variable, and estimates the
probability of occurrence of an event by fitting data to a logistic curve.
There are two models of logistic regression, binary logistic regression and
multinomial logistic regression. Binary logistic regression is typically used
when the dependent variable is dichotomous and the independent variables are
either continuous or categorical. When the dependent variable is not
dichotomous and is comprised of more than two categories, a multinomial
logistic regression can be employed. As an illustrative example, consider how
coronary heart disease (CHD) can be predicted by the level of serum cholesterol.
The probability of CHD increases with the serum cholesterol level. However, the
relationship between CHD and serum cholesterol is nonlinear and the probability
of CHD changes very little at the low or high extremes of serum cholesterol. This
pattern is typical because probabilities cannot lie outside the range from 0 to
1. The relationship can be described as an ‘S’-shaped curve. The logistic model is popular because the
logistic function, on which the logistic regression model is based, provides
estimates in the range 0 to 1 and an appealing S-shaped description of the combined effect of several risk
factors on the risk for an event (Kleinbaum & Klein, 2010).
logistic regression method is used for classification problems. Instead of predicting the values of response 0 & 1 as in linear regression will predict probability of response variables. making sure cure fitted in range of response variable as,
Y ∈ [0, 1]
x ∈ R
y = response variable
R = -ve ∞ to +ve ∞
The term logistic refers to
"logit" = "log odds"
ODDS
Odds of an event are the ratio of the probability that an event will occur to the probability that it will not occur. If the probability of an event occurring is p, the probability of the event not occurring is (1-p). Then the corresponding odds is a value given by,
odds = p/1-p
Let probability = P(Y=1|x) = p(x)
where 1 = it is not a number it is probability of class or category.
x ∈ R
P(x) ∈ [0, 1]
where p(x) = sigmoid function
p(x) =1/1+e-βx
Fig. 1 S -curve sigmoid function
Pic Courtesy: Wiki
above equation can be write as,
Parameter Estimation
goal is to estimate right hand side of above equation i.e β vector. logistic regression uses maximum likelihood for parameter estimation. let us see how does it works..
consider N samples with labels 0 and 1
for label 1 = estimate  such that P(x) is as close to 1 as possible
such that P(x) is as close to 1 as possible
for label 0 = estimate such that P(x) is as close to 0 as possible
such that P(x) is as close to 0 as possible
therefore for every sample we can write mathematically as
for 1 highest possible value =
for 0 lowest possible value =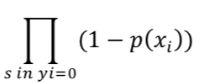
where xi is feature vector for ith sample
above equation is called as transcendental equation. The goal is to define the data which maximizes the function such that P(x) is as close to 1 as possible
such that P(x) is as close to 1 as possiblefor label 0 = estimate
 such that P(x) is as close to 0 as possible
such that P(x) is as close to 0 as possibletherefore for every sample we can write mathematically as
for 1 highest possible value =

for 0 lowest possible value =
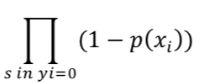
where xi is feature vector for ith sample
to estimate the log likelihood function take product of highest possible and lowest possible responses which must be maximum over all the elements of database.now log likelihood function will be as ,
further simplifying
now take log likelihood function and convert into summation,
put P(xi) back in above equation
now group Yi together
further simplifying we get,
Step By Step Execution of Algorithm
- Choosing a classification algorithm
Choosing an appropriate classification algorithm for a particular problem task requires practice each algorithm has its own quirks and is based on certain assumptions. To restate the "No Free Lunch" theorem no single classifier works best across all possible scenarios. In practice, it is always recommended that you compare the performance of at least a handful of different learning algorithms to select the best model for the particular problem, these may differ in the number of features or samples, the amount of noise in a dataset, and whether the classes are linearly separable or not. The five main steps that are involved in training a machine learning algorithm can be summarized as follows:
- Selection of features.
- Choosing a performance metric.
- Choosing a classifier and optimization algorithm.
- Evaluating the performance of the model.
- Tuning the algorithm.
Since the approach of this blog is to build machine learning knowledge step by step, main focus is on the principal concepts of the different algorithms.
- probabilities with logistic regression
Although the perceptron rule offers a nice and easygoing introduction to machine learning algorithms for classification, its biggest disadvantage is that it never converges if the classes are not perfectly linearly separable. Intuitively, the reason is as the weights are continuously being updated since there is always at least one misclassified sample present in each epoch. Of course, it can change the learning rate and increase the number of epochs, but be warned that the perceptron will never converge on this dataset. To make better use of our time, we will now take a look at another simple yet more powerful algorithm for linear and binary classification problems: logistic regression. Note that, in spite of its name, logistic regression is a model for classification, not regression.
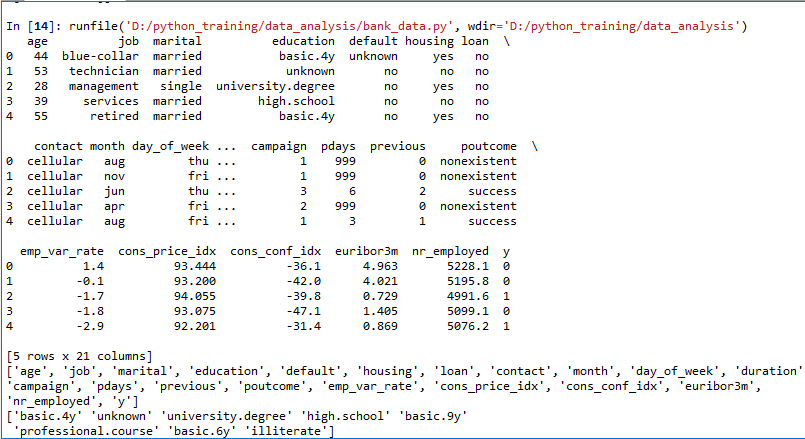
- DATA
The dataset comes from the UCI Machine Learning repository, and it is related to direct marketing campaigns (phone calls) of a Portuguese banking institution. The classification goal is to predict whether the client will subscribe (1/0) to a term deposit (variable y). The dataset can be downloaded from here.
fig. 2 code overview
photo Courtesy-www.quantinsti.com
- Input variables
- age (numeric)
- job : type of job (categorical: “admin”, “blue-collar”, “entrepreneur”, “housemaid”, “management”, “retired”, “self-employed”, “services”, “student”, “technician”, “unemployed”, “unknown”)
- marital : marital status (categorical: “divorced”, “married”, “single”, “unknown”)
- education (categorical: “basic.4y”, “basic.6y”, “basic.9y”, “high.school”, “illiterate”, “professional.course”, “university.degree”, “unknown”)
- default: has credit in default? (categorical: “no”, “yes”, “unknown”)
- housing: has housing loan? (categorical: “no”, “yes”, “unknown”)
- loan: has personal loan? (categorical: “no”, “yes”, “unknown”)
- contact: contact communication type (categorical: “cellular”, “telephone”)
- month: last contact month of year (categorical: “jan”, “feb”, “mar”, …, “nov”, “dec”)
- day_of_week: last contact day of the week (categorical: “mon”, “tue”, “wed”, “thu”, “fri”)
- duration: last contact duration, in seconds (numeric). Important note: this attribute highly affects the output target (e.g., if duration=0 then y=’no’). The duration is not known before a call is performed, also, after the end of the call, y is obviously known. Thus, this input should only be included for benchmark purposes and should be discarded if the intention is to have a realistic predictive model
- campaign: number of contacts performed during this campaign and for this client (numeric, includes last contact)
- pdays: number of days that passed by after the client was last contacted from a previous campaign (numeric; 999 means client was not previously contacted)
- previous: number of contacts performed before this campaign and for this client (numeric)
- poutcome: outcome of the previous marketing campaign (categorical: “failure”, “nonexistent”, “success”)
- emp.var.rate: employment variation rate — (numeric)
- cons.price.idx: consumer price index — (numeric)
- cons.conf.idx: consumer confidence index — (numeric)
- euribor3m: euribor 3 month rate — (numeric)
- nr.employed: number of employees — (numeric)
- Predict variable (desired target):
y — has the client subscribed a term deposit? (binary: “1”, means “Yes”, “0” means “No”)
Step 1
import all necessary libraries as,
output
Step 2
The education column of the dataset has many categories and we need to reduce the categories for a better modelling. The education column has the. Let us group “basic.4y”, “basic.9y” and “basic.6y” together and call them “basic”.
output
Step 3
Observations
The average age of customers who bought the term deposit is higher than that of the customers who didn’t. calculate categorical means for other categorical variables such as education and marital status to get a more detailed sense of our data. Now create dummy variables That is variables with only two values, zero and one.
Step 4
To get final data column write as,
output of final array
Step 5
Feature Selection
Recursive Feature Elimination (RFE) is based on the idea to repeatedly construct a model and choose either the best or worst performing feature, setting the feature aside and then repeating the process with the rest of the features. This process is applied until all features in the dataset are exhausted. The goal of RFE is to select features by recursively considering smaller and smaller sets of features.
output
Step 6
Model fitting into logistic regression algorithm and predict test results.
Step 7
Calculate the accuracy
output
The average accuracy remains very close to the Logistic Regression model accuracy; hence, we can conclude that our model generalizes well.
Step 8
confusion matrix
Output
The result is telling us that we have 10872+254 correct predictions and 1122+109 incorrect predictions
Logistic regression vs. other approaches
Logistic regression can be seen as a special case of the generalized linear model and thus analogous to linear regression. The model of logistic regression, however, is based on quite different assumptions (about the relationship between dependent and independent variables) from those of linear regression. In particular the key differences between these two models can be seen in the following two features of logistic regression. First, the conditional distribution is a Bernoulli distribution rather than a Gaussian distribution, because the dependent variable is binary. Second, the predicted values are probabilities and are therefore restricted to (0,1) through the logistic distribution function because logistic regression predicts the probability of particular outcomes rather than the probability of the outcomes themselves.
Logistic regression is an alternative to Fisher's 1936 method, linear discriminant analysis. If the assumptions of linear discriminant analysis hold, the conditioning can be reversed to produce logistic regression. The converse is not true, however, because logistic regression does not require the multivariate normal assumption of discriminant analysis
EXAMPLE 2
Dataset comes from the UCI Machine Learning Repository and it is related to Iris plant
database containing flower classes setosa, versicolor and virginica. Attributes are sepal
length sepal width and petal length, petal width
Step 1
import the required libraries as,
Step 2
Train the data set as,
Step 3
apply the logistic regression model
Output
Step 4
Make predictions and get the confusion matrix
Output
The result is telling us that we have 13+15 correct predictions and 0+2 incorrect predictions
Reference- Sebastian Raschka -Python Machine Learning







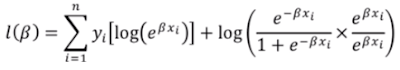






















No comments:
Post a Comment